Complex phase retrieval

import pandas as pd
from tramp.algos import EarlyStoppingEP
from tramp.experiments import BayesOptimalScenario, qplot, plot_compare_complex
from tramp.models import glm_generative

Model

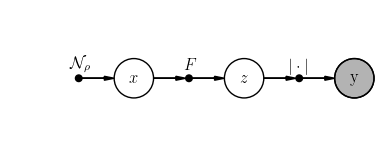
We wish to infer the sparse complex signal \(x \sim \mathcal{N}_\rho(.) \in \mathbb{C}^N\) from \(y = | Fx | \in \mathbb{R}_+^M\), where \(F \in \mathbb{C}^{M \times N}\) is a Gaussian random matrix.

model = glm_generative(
    N=1000, alpha=2, ensemble_type="complex_gaussian",
    prior_type="gauss_bernoulli", output_type="modulus",
    prior_mean=0.01, prior_rho=0.5
)
scenario = BayesOptimalScenario(model, x_ids=["x"])
scenario.setup(seed=42)
scenario.student.plot()

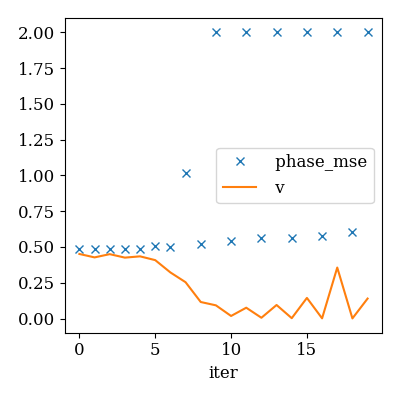
EP dynamics. Damping is essential !

ep_evo = scenario.ep_convergence(
    metrics=["mse", "phase_mse"], max_iter=20  # no damping
)
qplot(
    ep_evo, x="iter", y=["phase_mse", "v"],
    y_markers=["x", "-"], y_legend=True
)
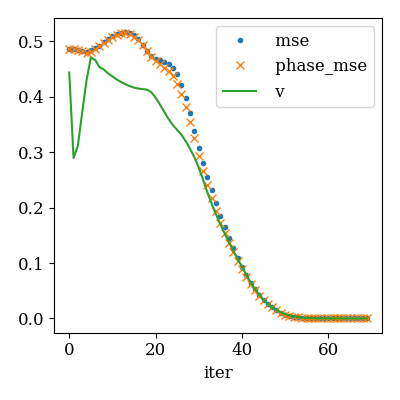
ep_evo = scenario.ep_convergence(
    metrics=["mse", "phase_mse"], max_iter=70, damping=0.3
)
qplot(
    ep_evo, x="iter", y=["mse", "phase_mse", "v"],
    y_markers=[".", "x", "-"], y_legend=True
)

• 
• 

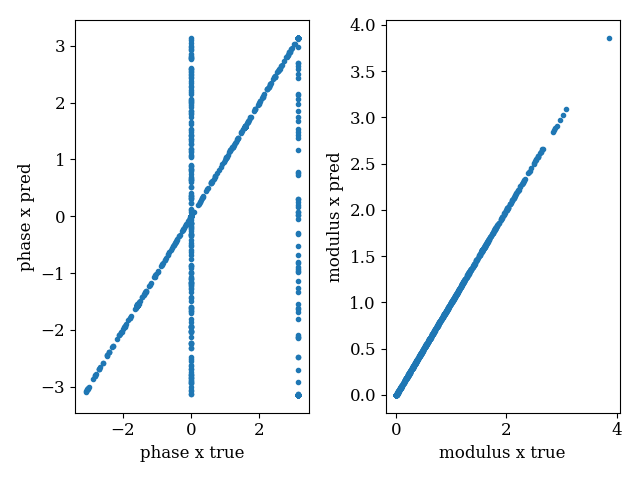
Recovered signal (up to a global phase)

plot_compare_complex(scenario.x_true["x"], scenario.x_pred["x"])

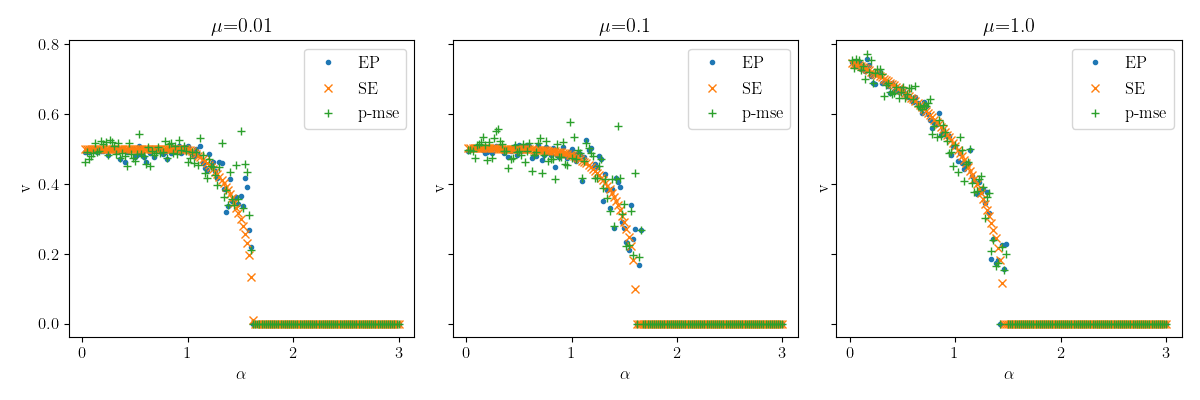
Compare EP vs SE

See data/phase_retrieval_ep_vs_se.py for the corresponding script.

rename = {
    "alpha": r"$\alpha$", "prior_mean": r"$\mu$", "prior_rho": r"$\rho$",
    "n_iter": "iterations", "source=": "", "phase_mse": "p-mse",
    "a0=0.1": "uninformed", "a0=1000.0": "informed"
}
ep_vs_se = pd.read_csv("data/phase_retrieval_ep_vs_se.csv")
qplot(
    ep_vs_se.query("source!='mse'"), x="alpha", y="v", marker="source", column="prior_mean",
    rename=rename, usetex=True
)
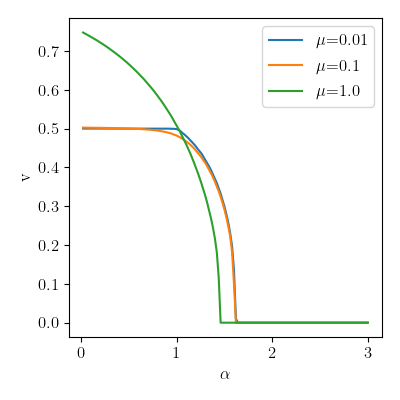
qplot(
    ep_vs_se.query("source=='SE'"),
    x="alpha", y="v", color="prior_mean",
    rename=rename, usetex=True
)
qplot(
    ep_vs_se.query("source=='SE'"),
    x="alpha", y="n_iter", color="prior_mean",
    rename=rename, usetex=True
)

• 
• 
• 

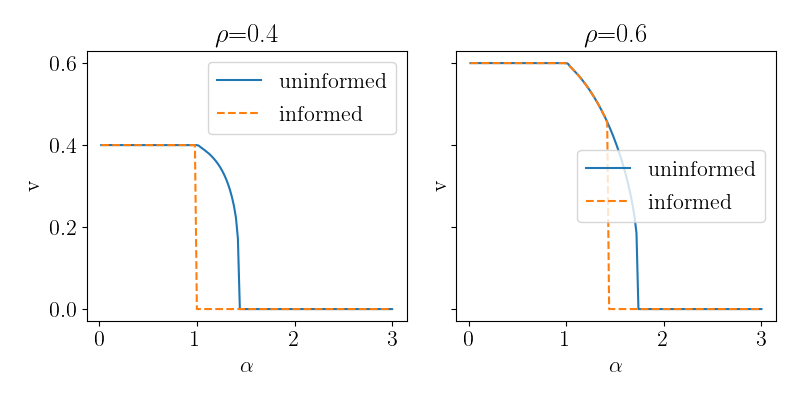
Phase transition

mse_curves = pd.read_csv("data/phase_retrieval_mse_curves.csv")
qplot(
    mse_curves, x="alpha", y="v", linestyle="a0", column="prior_rho",
    rename=rename, usetex=True, font_size=16
)