Sparse FFT

from tramp.algos import EarlyStoppingEP
from tramp.variables import SISOVariable as V, SILeafVariable as O, MILeafVariable, SIMOVariable
from tramp.channels import DFTChannel, GaussianChannel
from tramp.priors import GaussBernoulliPrior, GaussianPrior
from tramp.experiments import TeacherStudentScenario
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rc
rc('text', usetex=True)
rc('font', family='serif', size=24)

Define a Sparse FFT teacher

class SparseFFT_Teacher():
    def __init__(self, N, noise_var):
        self.t = np.linspace(-2*np.pi, 2*np.pi, N, endpoint=False)
        self.channel = GaussianChannel(var=noise_var)

    def sample(self, seed=None):
        if seed:
            np.random.seed(seed)
        x = np.cos(self.t) + np.sin(2*self.t)
        z = DFTChannel(real=True).sample(x)
        y = self.channel.sample(x)
        return {"x": x, "z": z, "y": y}

    def info(self):
        "Empirical estimates of var(x), var(z) and sparsity of z on a sample"
        s = self.sample()
        x , z = s["x"], s["z"]
        nonzero = (np.abs(z) > 1e-11)
        print(
            f"On a teacher sample : var(x)={x.var():.3f} "
            f"rho(z)={nonzero.mean():.3f} var(z)={z[nonzero].var():.3f}"
        )

Define a sparse FFT student

def build_sparse_fft_student(N, prior_var, rho, fft_var, noise_var):
    x_shape = (N,)
    z_shape = (2, N)
    student = (
        GaussianPrior(size=x_shape, var=prior_var) @
        SIMOVariable(id="x", n_next=2) @ (
            GaussianChannel(var=noise_var) @ O("y") + (
                DFTChannel(real=True) +
                GaussBernoulliPrior(size=z_shape, var=fft_var, rho=rho)
            ) @
            MILeafVariable(id="z", n_prev=2)
        )
    ).to_model()
    return student

Plotting function

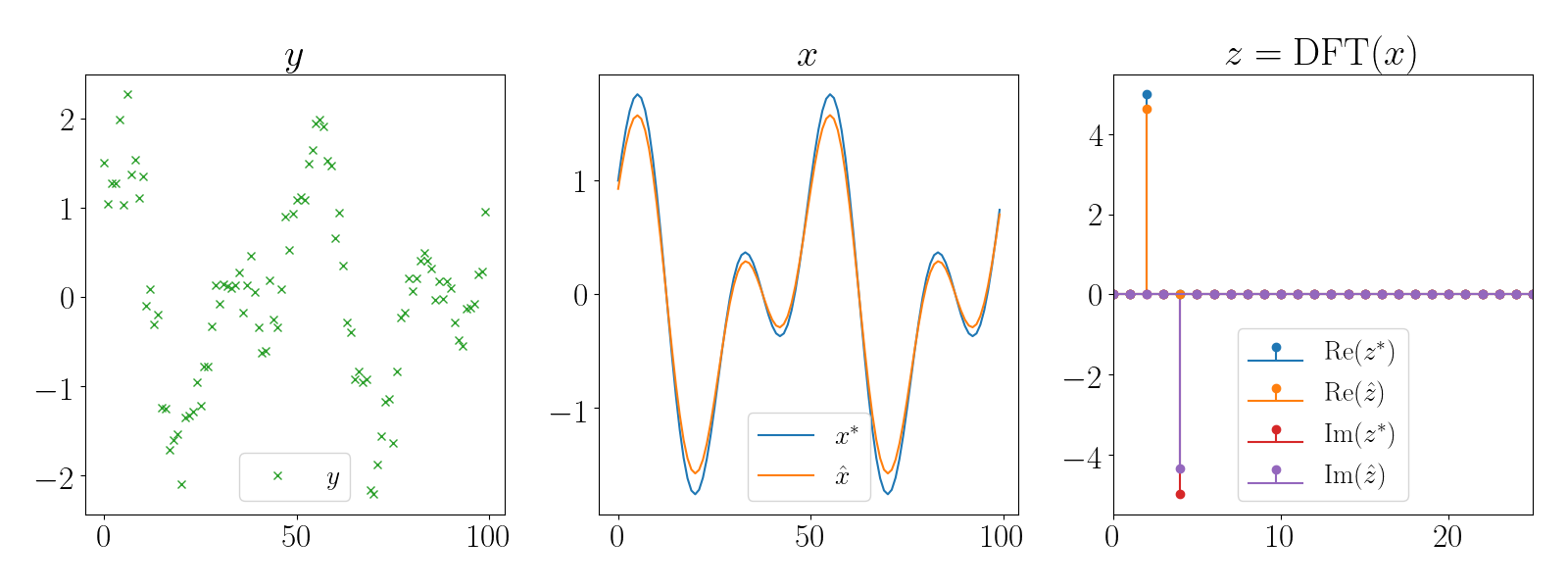
def plot_sparse_fft(scenario):
    fig, axes = plt.subplots(1, 3, figsize=(16, 6))
    axes[0].plot(scenario.observations["y"], 'C2x', label=r'$y$')
    axes[0].set_title(r'$y$')
    axes[1].plot(scenario.x_true["x"], label=r'$x^*$')
    axes[1].plot(scenario.x_pred["x"], label=r'$\hat{x}$')
    axes[1].set_title(r'$x$')
    axes[2].stem(
        scenario.x_true["z"][0], label=r"$\textrm{Re}(z^*)$",
        markerfmt="C0o", linefmt="C0-", basefmt="C0", use_line_collection=True
    )
    axes[2].stem(
        scenario.x_pred["z"][0], label=r"$\textrm{Re}(\hat{z})$",
        markerfmt="C1o", linefmt="C1-", basefmt="C1", use_line_collection=True
    )
    axes[2].stem(
        scenario.x_true["z"][1], label=r"$\textrm{Im}(z^*)$",
        markerfmt="C3o", linefmt="C3-", basefmt="C3", use_line_collection=True
    )
    axes[2].stem(
        scenario.x_pred["z"][1], label=r"$\textrm{Im}(\hat{z})$",
        markerfmt="C4o", linefmt="C4-", basefmt="C4", use_line_collection=True
    )
    axes[2].set_title(r'$z = \textrm{DFT}(x)$')
    axes[2].set_xlim(0, 25)
    for axe in axes:
        axe.legend(fancybox=True, shadow=False, loc="lower center", fontsize=20)
    fig.tight_layout()

Parameters

N, rho, noise_var, seed = 100, 0.02, 0.1, 1
prior_var, fft_var = 1, 18.75

We create the teacher student scenario

teacher = SparseFFT_Teacher(N, noise_var)
teacher.info()
student = build_sparse_fft_student(N, prior_var, rho, fft_var, noise_var)
scenario = TeacherStudentScenario(teacher, student, x_ids=["x", "z"])
scenario.setup(seed=seed)

Out:

On a teacher sample : var(x)=1.000 rho(z)=0.020 var(z)=18.750

Run EP

_ = scenario.run_ep(
    max_iter=1000, damping=0.1, callback=EarlyStoppingEP(tol=1e-2)
)

Plot

plot_sparse_fft(scenario)